Formula to Find Bearing or Heading angle between two points. Bearing or heading angle is used to define navigation generally in the field of aircraft or marine or Vehicle navigation or while working for land surveying. So what’s the heading or bearing? How we can find bearing between the two points on earth, with the formula? Or How we can find the other point, when one point, actual traveled distance and bearing is given? Let us discuss all this points, followed with the example and experiment with the tool for calculating bearing provided in the post.

Explore Route Compass Mobile App and calculate bearing angle using mobile phone. Download the app grab the new offers.
For More details connect us at support@igismap.com.
Bearing Calculator GIS Tool
- Route Compass – Bearing Angle Tool : This tool will help you to create a Route through Bearing angle and Distnace which can be used by many different applications.
Bearing can be defined as direction or an angle, between the north-south line of earth or meridian and the line connecting the target and the reference point. While Heading is an angle or direction where you are currently navigating in. This means to reach a particular destination you need to adjust your heading direction with the bearing. Generally a ‘compass’ is an instrument, which gives you the direction information for navigation. You must refer Haversine distance formula before going through this post.
Calculating Bearing or Heading angle between two points:
So if you are from GIS field or dealing with GIS application, you should know bearing and how to calculate bearing with formula. Let us look on formula and tool for bearing:
- Let ‘R’ be the radius of Earth,
- ‘L’ be the longitude,
- ‘θ’ be latitude,
- ‘β‘ be Bearing.
Denote point A and B as two different points, where ‘La’ is point A longitude and ‘θa’ is point A latitude, similarly assume for point B. Bearing would be measured from North direction i.e 0° bearing means North, 90° bearing is East, 180° bearing is measured to be South, and 270° to be West.
Note: If bearing is denoted with +ve or –ve initials whose values lies between 0° to 180°, then –ve is denoted for South and West sides.
Formula to find Bearing, when two different points latitude, longitude is given:
Bearing from point A to B, can be calculated as,
β = atan2(X,Y),
where, X and Y are two quantities and can be calculated as:
X = cos θb * sin ∆L
Y = cos θa * sin θb – sin θa * cos θb * cos ∆L
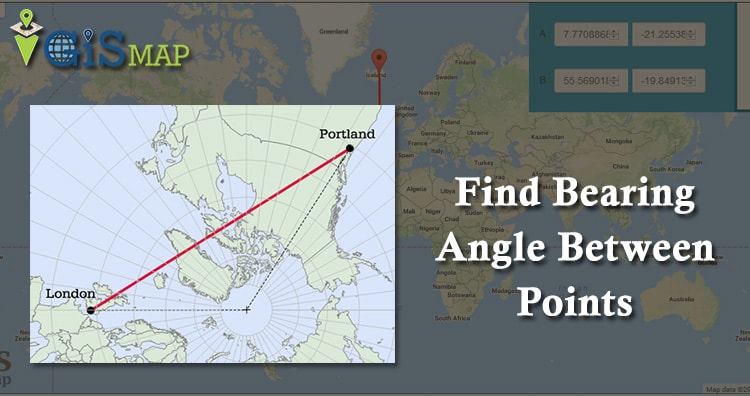
Lets us take an example to calculate bearing between the two different points with the formula:
- Kansas City: 39.099912, -94.581213
- St Louis: 38.627089, -90.200203
So X and Y can be calculated as,
X = cos(38.627089) * sin(4.38101)
X = 0.05967668696
And
Y = cos(39.099912) * sin(38.627089) – sin(39.099912) * cos(38.627089) * cos(4.38101)
Y = 0.77604737571 * 0.62424902378 – 0.6306746155 * 0.78122541965 * 0.99707812506
Y = -0.00681261948
***Convert θ into radians***
So as, β = atan2(X,Y) = atan2(0.05967668696, -0.00681261948) = 1.684463062558 radians
convert it into degree
β = 96.51°
This means, from Kansas City if we move in 96.51° bearing direction, we will reach St Louis.
You can also check video explanation of bearing angle.
Tool to find bearing angle between two lat lon points:
Check out the following IGISMap tools to work with Bearing Angle
IGISMap Bearing Angle Tool
IGISMap is a GIS based web platform providing multiple GIS applications that are most important in the field of geospatial analytics. The peculiarity of IGISMAP in the GIS Industry is its UI/UX that helps the user to perform effortless geospatial operations.
Bearing Angle tool of IGISMap can be used to create geospatial path based on bearing angle, distance and location. A path will be one or more straight lines connected between points plotted in order. User can plot required locations by simply clicking on the map or by entering address or coordinates. The path created in Bearing Angle will be available as GIS layer in the IGISMap. This GIS layer can be downloaded as GIS data in any format such as Shapefile, GeoJSON, CSV or KML.
Check https://routecompass.mapog.com to open Bearing Angle
Formula to find a lat lon point, when bearing, distance and another lat lon is given
Let us assume a condition, where you want to find out the where will an Airplane will land up, if you have following details of that Airplane, i.e actual distance it will travel, the bearing and the starting point (lat,lon)?
- Let first point latitude be la1,
- longitude as lo1,
- d be distance,
- R as radius of Earth,
- Ad be the angular distance i.e d/R and
- θ be the bearing,
Here is the formula to find the second point, when first point, bearing and distance is known:
- latitude of second point = la2 = asin(sin la1 * cos Ad + cos la1 * sin Ad * cos θ), and
- longitude of second point = lo2 = lo1 + atan2(sin θ * sin Ad * cos la1 , cos Ad – sin la1 * sin la2)
You may find both the tool on separate page, with Google map working on it: (It will be update in 2 days, please visit us again)
- Tool to Find Bearing, when two points are given
- Tool to find other point, when bearing, distance and one of the point is given.
I hope this article will definitely help you, to find the bearing or heading. You are free to share more data related to bearing or any thing that you uses to calculate bearing and how you use navigation with bearing.
If you find anything difficulty to understand the bearing calculation, you may comment below, so that we will discuss further on finding bearing or heading angle.
Sign up and login to MAPOG Tool to check more GIS tools.
Now we are on Youtube also. Please Like, Share and Subscribe our Channel IGIS Map

I am surveyor need some help calculate bearing formula
Kursgrade beginnen im Norden und im Uhrzeigersinn
Technische gegen Uhrzeigersinn 0 rechts auf x Achse.
Wie bekomm ich also Kurswinkel in Technisch
I trying to understand the derivation of X and Y.
I understand how the bearing is given in Radians as β = atan2(X,Y)
My understanding is that here X is the long difference and Y is the lat difference.
What I don’t understand is why long diff isn’t just PointBLong – PointALong
in other words,
X = -90.200203 – ( -94.581213) = 4.38101
Y = 38.627089 – 39.099912 = -0.472823
then β = atan2( 4.38101, -0.472823)
What am I missing?
Long diff varies with how far from equator toward the pole you are, in other words varies with latitude. I think the X and Y are actually reversed in the above derivation. It works for me but only when I reverse them within the argument of the ATAN2 function. Maybe Akshay could comment on this, please. Also, in the Haversine distance formula referenced (linked) above, the delta lat and delta long formulas use point #1 minus point #2 instead of traditional delta values where the first value is subtracted from the second (i.e. point #2 minus point #1). The simple way to see these derivations is to understand that the polar coordinates of lat/long are first converted to cartesian (X, Y, Z) where the polar direction of lat/long is parallel to the cartesian Z direction, +X points to 0,0 lat/long and +Y points to 0, +90 lat/long. The cartesian are then the typical or common Earth-centered coords. A diagram of this will show why a Latitude-dependent coefficient or multiplier term must accompany Longitude, since the distance subtended at Earth’s surface by some fixed angle of longitude changes with the latitude where that distance is measured. At North or South poles, that distance will become zero as all longitudes collapse to the same point, the pole. Along the Equator, that distance will be its maximum as the lat-dependent coefficient equals unity.
Here’s another method;
Distance & Azimuth from Position to Destination
Distance = 90 – Sin-1(sin(Destination Latitude) x sin(Your present Latitude) + cos(Destination Latitude) x cos(Your present Latitude) x cos(Difference in Longitude between Your Location and Destination Location)
Multiply answer by 60 to get Nautical miles.
Another way
Distance = 60 x Cos-1(sin(Destination Latitude) x sin(Your present Latitude) + cos(Destination Latitude) x cos(Your present Latitude) x cos(Difference in Longitude between Your Location and Destination Location)
Azimuth to Destination
NOTE- LHA= Present Longitude – Destination Longitude
Z = tan-1(sin (LHA) / (cos (LHA) x sin(Your present Latitude) – cos(Your present Latitude) x tan(Destination Latitude))
Then to put Z into the right quadrant, apply the following rules-
If answer is negative, add 180º to Z
LHA is NEGATIVE if it’s less than 180º .
Another way
tan-1(sin(LHA) / (cos(Present Latitude) x tan(Destination Latitude) – (sin(Present Latitude) x cos(LHA))
-continued on next page-
If LHA is greater than 180 it’s treated as a negative quantity.
If the Azimuth angle as calculated is negative, add 180 to it.
Really thank. I found this bearing formula very useful.
The values that I got according to formulation for x and y are different!!
X = cos(38.627089) * sin(4.38101) = -0.566840755 but not 0.05967668696
Y = cos(39.099912) * sin(38.627089) – sin(39.099912) * cos(38.627089) * cos(4.38101) = 0.32763159818398435 not -0.00681261948
I had the same problem but I could figure out what was wrong. You have to convert your Lats and Longs to Radiant to get the correct results.
Hopefully this helps.
Greetings
I got the same result with you. But not the same with the author
This is for excel
=(ATAN((COS(Lat2)*SIN(Lon2-Lon1)/(COS(Lat1)*SIN(Lat2)-SIN(Lat1)*COS(Lat2)*COS(Lon2-Lon1)))))*180/PI()
It works
Thanks for the formula, but I still do not get the correct bearing angle. It seems to me it is usually simpler to insert a function to convert Lat/Lon to UTM coordinates (where all values are positive long integers) and work with meters on a projected plane rather than decimal degrees or DMS, at least for distances that don’t require navigating a great circle.
Thanks for the excel formula. That is awesome. A couple extra points.
1. You need to convert lat and lon to radians before using the formula. RADIANS function
2. The answer in degrees bearing.
3. The bearing is from point 2 to point 1.
Not made clear in the tutorial, but the delta of the longitudes should also be converted to radians, not only the thetas.
Hi..
thanks for the formula, but I have a question,
the resulting bearing angle, we should use it from the geographical North right?
not the magnetic north?
thanks in advance
This formula is the conversion from a pair of
[φ1, λ1, r ] , [φ2, λ2, r] spherical coordinates [latitude, longitude, earth radius] to
d, θ where d is the angle at the centre of the earth between the points multiplied by the earth radius and θ is the angle of the arc on the surface compared to True North.
The calculation of magnetic variation [magnetic north difference from True north] is different at every location on earth, but can be calculated here.
https://www.ngdc.noaa.gov/geomag/calculators/magcalc.shtml#declination
Try this for Kansas City
https://www.ngdc.noaa.gov/geomag-web/calculators/calculateDeclination?lat1=39.099912&lon1=-94.581213&elevation=0&elevationUnits=F&model=WMM&startYear=2020&startMonth=2&startDay=28&resultFormat=html
How can I plug this into a calculator after I’ve found my X and Y values?
Thank you very much indeed for the clear and detailed explanation.
how can I calculate the latitude and longitude values using “2 line element” values or 11 level points
Would someone please explain why the following set of coordinates (a to b, and c to d) have relatively similar direction but the bearing angles are so different?
a: (39.099912, -94.581213)
b: (38.627089, -90.200203)
bearing angle from a to b is 96.513
c: (48.35, -122.65)
d: (26.2697, 50.6260)
bearing angle from c to d is 6.244
Thanks
Because the shortest route [great circle on a sphere] from Vancouver to Bahrain almost goes over the north pole.
Further,
From 122°W to 50°E is almost diametrically opposite on the globe [172° difference]. So the resultant direction is ALMOST along a meridian of longitude [Obviously 6° different!!] and via the Polar Region. If destination had been 58°E it would be due north/south and over the geographic pole.
Very nice! Your formulas are very easy to do. I suggest you to include other technical formulas like haversine formula. Bye
hello
have did you calculat this atan2(x,y) ?
hello
have did you calculate atan2(x,y) ?
thank you
what does the letter a preceding tan refer to ie, what’s the difference between tan and atan ? and between sin and asin ?
atan means inverse of tangent or its a arctan
∆L is never explained. It’s actually = ( Latitude B – Latitude A)
also you need to convert every number within cos and sin brackets to radians.
so this is NOT true:
X = cos(38.627089) * sin(4.38101)
X = 0.05967668696
but THIS is true
X = cos(38.627089*π/180) * sin(4.38101*π/180)
X = 0.05967668696
same applies for the second formula for Y
Dear Akshay,
Thank you for very good examples. I have implemented your bearing between two points calculation and it works fine for your example of flying from Kansas City to St. Louis: β = 96.51°. However, your equations do not work if we will fly back – from St. Louis to Kansas City. I would expect that bearing will be
180°+96.51° = 276.5126°. Your equation produces -80.7376°. Even if we will add this negative this value to 360° it will produce 279.2624°.
Apparently something is missing. Please advise.
Best wishes,
Oleg
Oleg,
The great circle route is not a line of constant heading (except along the equator or due North/South). The heading on the route from Kansas City to St Louis STARTS as 096.51° at Kansas City, but it will be 99.26° as you arrive at St Louis. The reverse direction will be 279.26° at St Louis and 276.51 as you arrive at Kansas City. This is because on a sphere the “straight line” is a curve on the earth’s surface [a curve at constant radius from the earth’s centre].
A great circle is the shortest track on the earth’s surface between the two points on the surface which also cuts through the earth’s centre [this would leave two perfectly equal hemispheres and not a smaller and bigger part]. Unfortunately, the direction shown in the calculation is relative to “North” and North is a different direction in 3D from any start point and converges on the geographic pole [travel North from any location on earth and you will eventually arrive at the North Pole. Although two people with different starting points would meet at the pole they would be coming from different directions!].
On a map [which is not a globe] the great circle between any two points in the same hemisphere which are not North/South curve towards the nearest Pole. Try this on Google Earth, using the ruler to draw a line and read the heading [it is easy to visualise on longer distances when the earth is obviously a spheroid, like from Sacramento [38.7N, 121.6W] to Washington DC [38.85N, 77.04W]]. Turn on the Latitude/Longitude grid [CTRL-L] and you can see the track will cross 40°N twice and nearly reach 41°N in Central Nebraska .
FYI, Sacramento to Washington starts at 075° [ENE] and arrives at Washington at 104° [ESE].
Ray,
You didn’t understand Oleg’s question. It’s not a great circle issue. It is a quadrant issue. Even the original example comes up with -6.51 not 95.51. None of these equations work in all situations and have to be “adjusted” by quadrant due to the fact that the cos/sin formulas give the same answer for different angles, i.e.: sin(30 degrees) = sin(150 degrees).
hi good ofter noon
i have problem with 4 point if checked between 1.2.3 is ok when i checked nober 4 coming wrong
but if i fix total sation in nober 1 is coming nomber 4 ok
Simply to say thanks for the heads-up on igismap.
It completely solved my problem finding the precise heading to a television transmitter.
The X and Y formulas are inverted and result in the wrong answer.
Do ONE or the OTHER:
1) atan2 (Y, X)
or
Y = cos θb * sin ∆L
X = cos θa * sin θb – sin θa * cos θb * cos ∆L
Thanks, that solves my issue with bearing in excel.
Thank you Charles. Solved my problem in OpenOffice Calc too.
Request bearing and distance from 23.8243° N 90.4129° E to 23.8071° N 90.3634° E
Hello , Must say a very useful formula to find heading angle , thank you – trying to solve agriculture domain use case here with the same
Have one small query here , I am getting positive heading angle ( 159.5292) where as from the tool : https://www.igismap.com/map-tool/bearing-angle
I am getting head angle as negative ( -159.529o ).
Could you please guide me here , what I am missing here , thanks again
# R Programming
library(pracma)
longitudeA <- as.numeric(deg2rad(-0.772383960000))
latitudeA <- as.numeric(deg2rad(53.507616240000))
longitudeB <- as.numeric(deg2rad(-0.772915460000))
latitudeB <- as.numeric(deg2rad(53.506769480000))
X = cos(latitudeB)*sin(abs(longitudeB-longitudeA))
Y = (cos(latitudeA)*sin(latitudeB))- (sin(latitudeA)*cos(latitudeB)*cos(abs(longitudeB-longitudeA)))
bearingAngle <- atan2(X,Y)
bearingAngle <- rad2deg(bearingAngle)
print(bearingAngle) # 159.5292 is not coming negative
very good
i don’t understand the unit of the x and y. Are they in radian or degree.
How the formulas for X and Y are derived?
is there any simpler formula to find bearing angle ?
Hi, got there in the end but had to swop X and Y around to get the degree of 96.51.
My next point is, when I input differant points in the UK ie, 53.360883 -0.738307 and 51.1085064 1.138575 I get a bearing of 128.25 from the calculation, but using the map tool bearing angle the result is 152.218 deg which is more correct, why do I get a lower bearing from the calculation?
In regard to converting degrees (or other angle measurement) to radians, the conversion should be matched to the units the sin() or cos() function are expecting, which for the programing languages I’ve used are radians. Calculators, on the other hand, will usually expect angles in degrees (although some calculators will let you set the units.
In regard to argument order for the atan2() function, I’ve encountered both: Excel ATAN2(a,b) is analogous to atan(a/b) [or arctan(a/b) or inverse tan(a/b). For C/C++ & Python atan2(a,b) is analogous to atan(b/a), etc. Atan2 is useful because you don’t have to provide a special case for atan(1/0), where the divide by zero causes errors.
Another note: be aware of the direction of zero bearing that you’re working with! Most math functions assume 0 degrees is along the positive X axis (“east”) with positive angles proceeding clockwise. “Bearings” often (but depending on local custom) assume 0 degrees is along the positive Y axis (“north”) with positive angles proceeding counter-clockwise. For example, surveyors in the continental U.S. measure azimuth (the surveyors’ term for bearing) clockwise from the north; in Hawaii, azimuth is measured from the south (don’t remember whether clockwise or counter).
Finally, as mentioned before, the bearing from A to B will differ from the bearing from B to A, unless A & B are both on the equator or on the same meridian. This is because the meridians are parallel to each other only at the equator.
Oops – error in my post! “Most math functions assume 0 degrees is along the positive X axis (“east”) with positive angles proceeding >>> counter-<<<clockwise."
Also, the square bracket "[" in the ATAN2 discussion should be removed.
For the bearing between two points, the atan2 function always has atan2(y,x) argument ordering, expressly _not_ atan2(x,y). So what you’re calling “x” should be called y, and what you’re calling “y” should be called x, so that atan2 code is the proper atan2(y,x) call.
For those interested, the formula to find a lat lon point, when bearing, distance and another lat lon is given translates to an excel formula like so:
Lat2 =DEGREES(ASIN(SIN(RADIANS(Lat1))*COS(Distance Km/6371) + COS(RADIANS(Lat1))*SIN(Distance Km/6371)*COS(RADIANS(Angle))))
Lon2 =DEGREES(RADIANS(Lon1)+ ATAN2(COS(Distance Km/6371)-SIN(RADIANS(Lat1))*SIN(RADIANS(Lat2)), SIN((RADIANS(Angle))*SIN(Distance Km/6371)*COS(RADIANS(Lat1))))